Winkelteilung

Winkelteilungen

Wer schon einmal versuchte, einen Winkel geometrisch zu dritteln, weiß, dass das nicht leicht möglich ist, mit Zirkel und Lineal allein gar nicht geht.
Eine alte Methode stammt von Archimedes, nachzulesen z.B. bei Wikipedia. Diese bitte ich nachzuschlagen und sich zu Gemüte zu führen. Betrachtet man das zugehörige Bild, kann man leicht bemerken, dass es sich sinnvoll verlängern lässt, siehe Geogebra unten:
(Die Geogebras zu diesem Thema gibt es als Arbeitsblätter zum Download hier.)

Bewege mit C den Winkel in A. Schaue, wie sich wann genaue Kreisteilungen ergeben. Welche Form die Schere gleicher Radien je zeigt.
Beachte, wie sich die Radienscheren verhalten. Immer bilden sie gleichschenklige Dreiecke.
Der außerhalb des Kreises liegende 2. Basiswinkel des innersten blauen Dreiecks ist natürlich ebenfalls α.
Für den Winkel in der Spitze bleiben dann 180°-2α. Dessen Nebenwinkel hat folglich auch den Wert 2α.
Er ist Basiswinkel des nächsten umgekehrten gleichschenkligen violetten Dreiecks, in dessen Spitze dann 4α zu 180° fehlen.
1α liegt zum innersten blauen Dreieck gehörig daneben auf der Grundlinie, bleiben für den Basiswinkel des nächstangrenzenden blauen Dreiecks 3α. Usw.
Die Winkel sind also – wenn vorhanden – nacheinander das doppelte, dreifache, vier-, fünf-, sechs-, siebenfache von α. Umgekehrt ist α ein entsprechender Bruchteil der äußeren Winkel.
Bringt man einen beliebigen Winkel mit dem entsprechenden Basiswinkel dieser Reihe zur Deckung, hat man die Bruchteile quasi geometrisch gegeben.
Es lässt sich also auf diese Art eine fast beliebige Winkelteilung vornehmen!

Und noch einmal anders, verändere per Schieberegler den Winkel β, damit dann α. Per Klick dicht neben den Punkt lässt sich das auf Hundertstel genau einstellen. Betrachte das braune Vieleck im Kreis, seine Zähligkeit:

Kreisteilung

Interessant sind nun alle Winkel, die eine genaue Kreisteilung ergeben. Das ist durch die in eins fallenden Punkte auf dem Kreis gut genau zu sehen.
Bei den vier kleinsten Teilungen durch 1,2,3 und 4 ergibt sich noch gar kein sichtbares Dreieck.
Die nächsten vier Teilungen haben je eines:

• Bei der Fünftelung ein erstes: 72° hat α, ein zweiter Radius kann den anderen Schenkel erreichen, der Radius klappt weit zurück, einen weiteren gibt es nicht.
• Mit der Sechstelung haben wir ein gleichschenkliges, sogar gleichseitiges Dreieck, von beiden Schenkeln aus fallen die Radien in eins zusammen.
• Die Siebtelung führt zu einer offenen Kreuzung der Radien und
• bei der Achtelung fallen sie im rechten Winkel auf die gegenüberliegenden Schenkel.

Über den rechten Winkel hinausgehend muss sich ein zweites Dreieck öffnen, das scheint evident.
Und so geht es in Gruppen von je 4 Teilern immer weiter:

• ein spitzes kommt mit der nächsten ungraden Teilung je dazu,
• mit der nächsten graden Teilung entsteht insgesamt ein gleichschenkliges Dreieck, wie bei der Sechstelung fallen die Radien von beiden Schenkeln aus in eins zusammen,
• wiederum folgt eine ungrade Teilung mit sich öffnenden Radien und
• mit den rechten Winkeln sind bei der folgenden graden Teilung die Möglichkeiten mit dieser Radienzahl erschöpft.

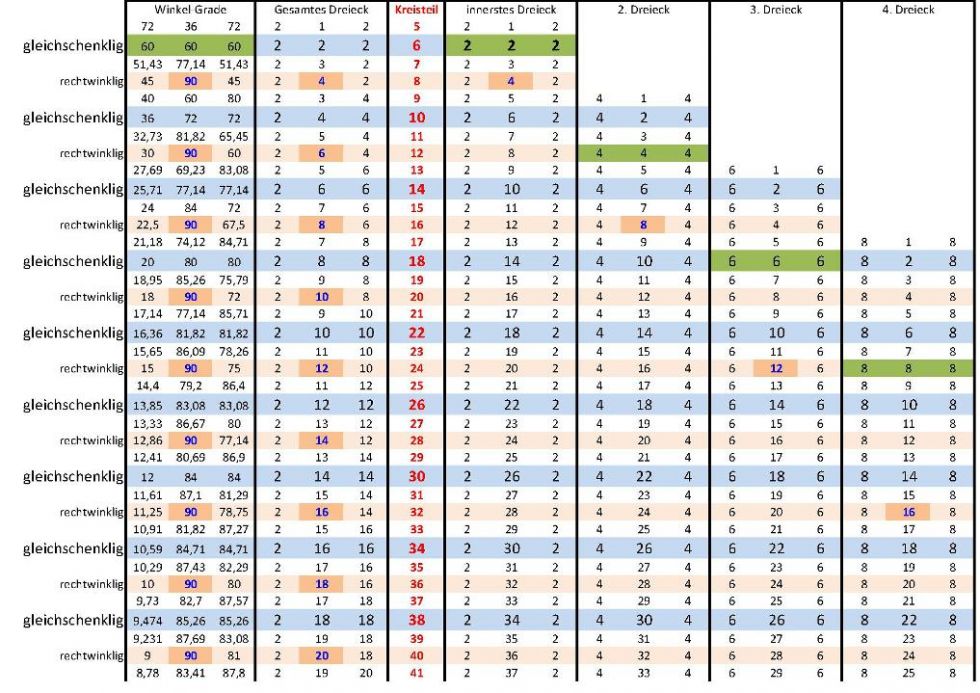
Ein interessantes Muster tut sich auf, im Excelinchen lässt es sich schön überblicken, in einer Formelgefüllten Zeile darf eine beliebige Teilerzahl eingegeben werden.
Damit auch ungrade Kreisteilungen glatte Zahlen ergeben, hat α in der Tabelle immer den Wert 2 bekommen (erste Spalte unter „Gesamtes Dreieck“). Die Reihe der Dreiecke hat also als innere Winkel nicht 1,2,3,4,5,6,7… also die Folge der natürlichen Zahlen, sondern die der ganzen natürlichen Zahlen 2,4,6,8…
Schön sind die Vierergruppen zu sehen, der Wechsel von Gleichschenkligen (blau) und Rechtwinkligen (braun) Gesamtdreiecken bei graden Teilungen. Alle 6 Reihen gibt es ein gleichseitiges Dreieck dazwischen (grün).

Werkzeug

Ein dingliches Werkzeug für den Geometer lässt sich damit so einfach leider nicht bauen, vielleicht einigermaßen genau je für eine Vierergruppe eben. Darüber hinaus müsste man ja sonst Radien einfügen oder herausnehmen, würde das Spiel, welches ein bewegliches Gestell sicher braucht, bald zu ziemlichen Ungenauigkeiten führen.

Oder umgekehrt: Für eine bestimmte Teilung werden zwei Stangen mit der entsprechenden Zahl von Radien im Zickzack lose verbunden, dann kann man am einen Ende den zu teilenden Winkel beliebig einstellen, am anderen Ende muss dann das Scherengelenk erst herbeigeschoben werden. Hier ein Beispiel, wie so etwas für eine Fünfteilung aussehen könnte: