Geometrische Metamorphosen

Geometrische Metamorphosen sind niemals echte im Goetheschen Sinne. Aber sie können solche abbilden, sie in ihren Grundprinzipien dadurch erlebbar machen. Und dies ob ihrer Gesetzmäßigkeit genauer als alle pflanzlichen oder tierischen Metamorphosen.

Eine Metamorphose ist eine Entwicklung. Über unterscheidbare Stufen hin zu einem Höheren, dass aber das Erste auf höherer Stufe ist, so einen Kreis schließt. In rhythmischem Spiel zwischen Polaritäten: Die mittleren Stufen verhalten sich polar zu beiden Enden, diese zueinander auch – je nach Perspektive.

Der Kreis:

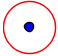
Als Vorspann soll betrachtet werden der Kreis: banalster Wicht und höchste Vollendung in einem. Im Gang durch die Formen der vier Grundrechenarten: Addieren, Subtrahieren, Multiplizieren, Dividieren.

Der Kreis als simple Konstante, allseitig gleiche Entfernung zu einem Mittelpunkt ist jedem klar und geläufig, unmittelbar.
Nimmt man den Mittelpunkt als Doppelpunkt, sind auch Summen der Abstände beider Doppelpunkte zu jedem Hüllpunkt gleich, das versteht sich von selbst – so ist der Kreis auch eine Ellipse! Im gleichen Sinn auch eine Hyperbel usw., was wäre er dann nicht!

Aber betrachten wir die Formen der Reihe nach.
(Weil Rudolf Steiner das schon einmal tat, biete ich hier die Gelegenheit, seine Worte zu lesen: der relvante Ausschnitt als pdf.
Oder der ganze Vortrag auf der Seite der Freien-Nachlass-Verwaltung-Rudolf-Steiner fnv-rs.net. Leider fehlen jeweils die zugehörige Bilder.)

Ellipsen:

– sind die Form der konstanten Summe.
Als Summe, zusammen, sind die Entfernungen eines jeden Hüllpunktes zu beiden Brennpunkten überall gleich. Was bedeutet, dass eine Schnur um jeden Ellipsenpunkt und beide Brennpunkte gezogen immer gleich lang ist: die „Gärtnermethode“ ist dadurch möglich.

Halte ich eine bestimmte Summe fest und bewege die beiden Brennpunkte, gibt es zwei Extreme: Haben die Brennpunkte fast keinen Abstand, erscheint fast wieder ein Kreis, mit Doppelpunkt als Zentrum, s.o.. Wird der Abstand zu groß, zerrinnt die Form zur gespannten Linie zwischen den Brennpunkten, dann ins Nichts – keine Hüllform bleibt.

Sehr schön lassen sich die Ellipsen ins Bild setzen mit Hilfe von Kreis-Scharen: ich zeichne um zwei Brennpunkte herum Scharen von Kreisen in stetigen Schritten: so, dass ihre Radien um immer den gleichen Betrag größer sind.
Liegen die Schnittpunkte zweier Kreise auf einer bestimmten Ellipse, dann tun es die Schnittpunkte „diagonal“ daneben auch: der eine Kreis ist ja um genau einen Betrag größer, der andere um den gleichen Betrag kleiner, ihre Summe ist also je gleich, der Schnittpunkt gehört zur selben Form. Mit ein wenig Übung kann man das schon an den simplen leeren Kreis-Scharen bemerken, füllt man überkreuz versetzt jeden zweiten Zwischenraum farbig, springen die Ellipsen direkt ins Auge:

Hyperbeln:

Im selben Bild zeigen die Kreisschnittpunkte andersherum verbunden richtig Hyperbeln – die zweiarmigen Formen der Subtraktion. Da gehe ich „diagonal“ von einem Schnittpunkt aus einen Schritt weiter so, dass die beiden nächstgrößeren Kreise sich schneiden, beide also um einen gleichen Betrag größer sind: so muss dann die Differenz ja wieder dieselbe sein.

(Bilde ich die Differenz immer in der gleichen Reihenfolge, ziehe also ab vom Abstand-zum-Punkt-A den Abstand-zum-Punkt-B, dann ist die eine Differenz freilich negativ. Nur im Betrag sind die beiden Differenzen gleich.)

Halte ich die beiden Brennpunkte fest und verändere die Differenz, gibt es zwei Extreme: Ist die Differenz gleich Null, erscheint die Hyperbel als Doppelgrade mittig zwischen den Brennpunkten. Ist die Differenz dem Brennpunktabstand gleich, fallen die Ast-Arme beidseits je vom Brennpunkt nach außen zum Strahl zusammen. Wenn die Differenz noch größer wird, fehlt wie im Falle der Ellipsen jede Hüllform.

Cassinische Kurven:

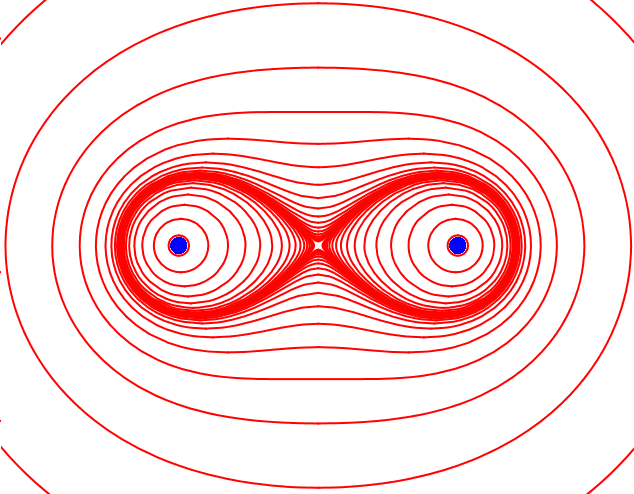
Hier wird es interessant: Suchen wir von zwei Brennpunkten aus ein konstantes Produkt, befinden sich die beiden Abstände in einem dynamischen Verhältnis zueinander, vervielfacht sich einer um einen bestimmten Faktor, verringert der andere sich um den gleichen Faktor.
Eine kompliziertere, differenziertere Formfamilie:
Ist das Produkt sehr klein oder sind in Relation die Brennpunkte sehr fern, erscheinen fast einzelne Kreise, leicht unrund. Dann bei größerem Produkt zwei Eiformen. Eine Mitte zwischen den beiden als gemeinsames Zentrum wird spürbar. Weiter folgt die Lemniskate, die liegende Acht – gedacht und zu denken in dreifacher Form:

als zwei sich spitz berührende Tropfen – von den zwei kleinen Einzelformen kommend
als eine überkreuz verlaufende flüssig zu zeichnende Kurve, die „Achterbahn“ eben
als bis zur Wespen-taillierung eingeschnürte Gesamtform – von außen kommend

Darüberhinaus gibt es weiter nur einheitliche Gebilde. Es entsteht zunächst eine eingeschnürte Form, weiter außen kann man sie kaum von einer Ellipse unterscheiden. Am Ende steht fast ein gemeinsamer Kreis um einen Doppelpunkt herum, ähnlich wie selbigen Falles bei der Ellipse.

Auch das lässt sich sehr schön mit zwei Kreis-Scharen veranschaulichen, jetzt solchen mit dynamischem Wachstum, jeder nächste Kreis ist um einen bestimmten Faktor größer.
Liegen die Schnittpunkte zweier Kreise auf einer bestimmten Cassinischen Kurve, dann tun es die Schnittpunkte „diagonal“ daneben auch: der eine Kreis ist ja um genau einen Faktor vergrößert, der andere um den gleichen Faktor verkleinert, ihr Produkt muss also je gleich sein:

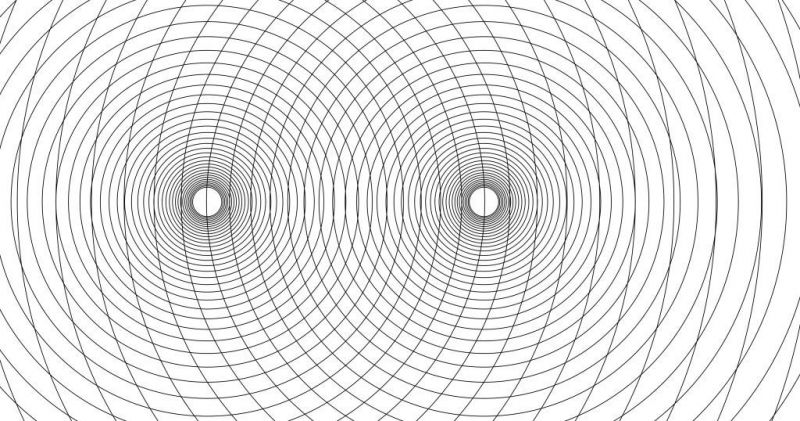
Divisionskreise:

Und wieder werden Gegenformen sichtbar, Verbindungslinien in der anderen „Diagonale“, richtig die Formen der Division, zweiarmig wieder – es so aufzufassen legt das Bild nah. Gehe ich von einem Schnittpunkt aus „diagonal“ einen Schritt weiter so, dass die beiden nächstgrößeren Kreise sich schneiden, beide also um einen gleichen Faktor vergrößert sind: so muss dann der Quotient ja wieder derselbe sein!

(Bilde ich das Verhältnis immer in der gleichen Reihenfolge, also als Abstand-vom-Punkt-A zum Abstand-vom-Punkt-B, dann ist das eine Verhältnis freilich der Kehrwert des anderen. Anders als bei der zweiarmigen Hyperbel ist noch nicht einmal der Betrag gleich. Insofern mag man diese Form zu Recht auch als einarmig betrachten?)

Halte ich die beiden Brennpunkte fest und verändere den Quotienten, gibt es zwei Extreme: Ist der Quotient gleich Eins, erscheinen die Kreise als Doppelgrade mittig zwischen den Brennpunkten – wie bei den Hyperbeln. Geht der Quotient gegen Null oder Unendlich, bleiben zwei winzige Kreise übrig bzw. gibt es eben gar keine Hüllform mehr.

Bei konstanter Division entstehen Divisionskreise. Ja, wieder Kreise! Kreise, gebildet ohne Mittelpunkt, als Form eines konstanten Quotienten!

Zu einem gegebenen Kreis kann jeder leicht den Mittelpunkt finden. Aus der Betrachtung einer Ellipse, Hyperbel oder Cassinische Kurve leuchtet es unmittelbar ein, dass es eindeutig definierte Brennpunkte gibt, mögen sie auch weniger leicht zu finden sein.

Anders als eine Ellipse, Hyperbel oder Cassinische Kurve ist ein einzelner Divisionskreis nicht nur von zwei ganz bestimmten Brennpunkten aus bildbar, sondern von allen. Weil er ein Kreis ist, allseitig gleich!
Das bedeutet, dass es zu jedem inneren (Brenn-)Punkt einen äußeren gibt, mit dem zusammen der Kreis gebildet werden kann. Auf diese Weise „spiegelt“ der Kreis die gesamte Umgebung in sich hinein und umgekehrt. Brennpunktpaare sind also genausogut Inversionspunkte am Kreis. (Kreise des Apollonius)
Ein vollständiger Divisionskreis ist dem Bild nach „zweiarmig“ wie die Hyperbel, besteht aus zwei gleichgroßen Kreisen. Und zwei solche Kreise zusammen haben als Partner selbstverständlich ein ganz bestimmtes Brennpunktpaar.

So sieht man also, wie Kreise etwas sehr verschiedenes sein können, je nach Betrachtungsart, Herleitung, Perspektive.

(Als „Nebenprodukt“ gibt es hier eine Betrachtung zum Thema „Beziehung, Verhältnis, Partnerschaft – was die Geometrie dazu lehren kann“: zum Artikel, oder als pdf.)

Unten ein „Geogebra“ als Veranschaulichung, hier kann jeder einige Möglichkeiten durchspielen.
Links oben gibt es Werkzeuge darin:

Ein Gang durch die Kegelschnitte:

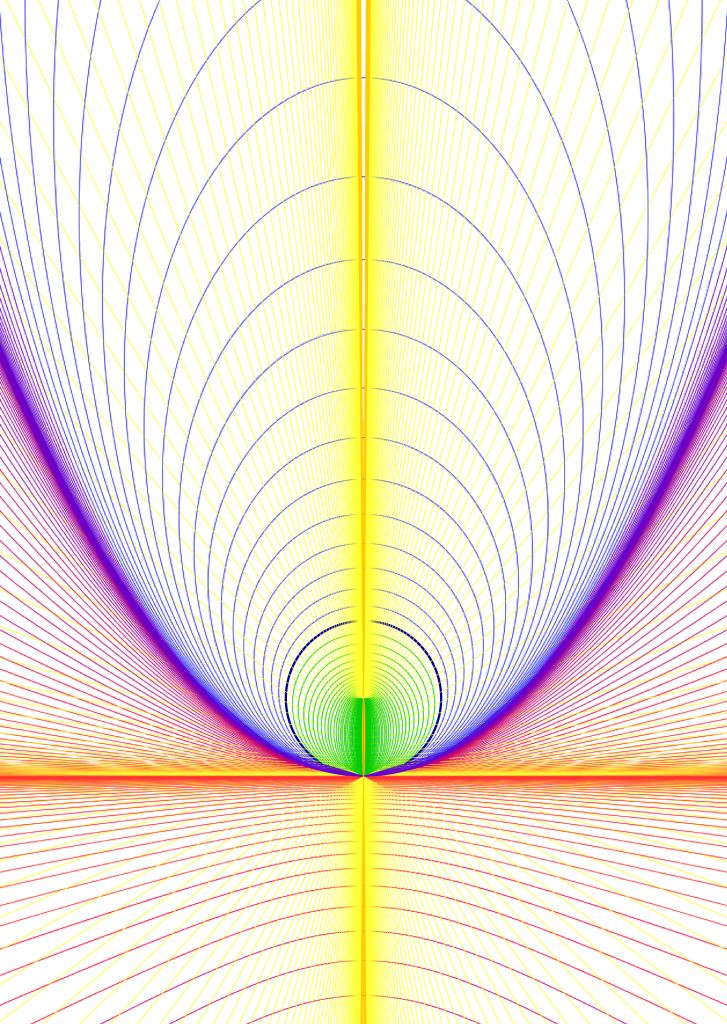
Die Familie der Kegelschnitte als Reihe zu erfahren, darauf kann leicht man kommen…

Der folgende Gang ist zuerst etwa 1996 bei Baukursen in Medewege, in Theoriestunden zum Thema „synthetische oder projektive oder lebendige Geometrie“ entstanden, hat mich einfach als schönes Gebilde weiter bewegt.
Erst Ostern 2010, anlässlich einer Karfreitagsfeier mit Haydens Musik zu den sieben letzten Worten Jesu und Bildern zu den planetarischen Siebenschritten ist mir ein möglicher Zusammenhang fühlbar geworden.
Diesen zunächst sehr geometrienah sichtbar zu machen habe ich die folgenden Seiten geschrieben zu Ostern 2010
Zum Artikel mit neuen Geogebras, sowie als pdf.

Weitere Formen:

Nun gibt es nicht nur die vier Grundrechenarten und so kann man sich fragen, wie wohl aussehen die Formfamilien zu einer konstanten Potenz oder einem konstanten Exponenten? Man kann dieses Thema spielerisch angehen duch Kreis-Scharen unterschiedlichsten Wachstums und all ihren Kombinationen: Was geschieht, wenn eine stetig wachsende Kreis-Schar mit einer dynamisch wachsenden sich überschneidet? Was, wenn verschiedene Wachs- oder Schrumpfarten gewählt werden? Ein paar Bilder sollen Möglichkeiten verdeutlichen:

Pascalsche Schnecken:

1990 zeigte mir der Maler Jürgen Dohmen ein geometrisches Verfahren zur Formumwandlung: mit einem Lineal-Ende nahm er eine beliebige Form ab, ließ es über ein Gleitlager laufen sozusagen, an seinem anderen Ende zeichnete ein eingespannt zu denkender Stift dann etwas Neues.
Diesem Verfahren bin ich dann auf den Grund gegangen, habe damit Kreise umgewandelt, mit einer ungeheuer reichhaltigen Wandlungsvielfalt im Ergebnis. Kreise wandelten sich zu Kreisen, über Eiformen und Lemniskatenähnliche, Einstülpungskringel und Bananen, auch Monde und Nasenmonde oder wie immer man die unbenamsten Formen neu nennen mag.
Damit zeigen die Pascalschen Schnecken in einer Reihe alle oben gesehenen Formen und noch viel mehr! Hier geht es zu einem eigenen Artikel mit vielen meditativen Geogebras dazu. Unten ein Beispiel:

Geometrische Meditationen