Beziehung, Verhältnis, Partnerschaft.

Was die Geometrie dazu lehren kann…
(Hier wird die der Ebene betrachtet, im Raum gilt Entsprechendes.)

Heute gilt:
Jeder Mensch ist ein Kreis – rund und vollständig, mit eigenem Zentrum, eigener Mitte. Bestenfalls lebt man sein Leben in wachsenden Ringen…
Ein Kreis aber ist auch ein banaler Wicht, geometrisch die Banalität schlechthin, konstanter Abstand vom innersten Punkt. Zwar auch perfekt. Aber fertig, abgeschlossen, er braucht keine Welt um sich herum. Einsam sehr.

Zwei solche Kreise können nun bei genügend Nähe eine Schnittmenge haben, schön. Ein Stück Welt gemeinsam, einen Teil Gemeinsamkeit. Dafür muss kein Kreis anders werden, jeder bleibt doch ganz allein.
Ohne das Stück gemeinsamer Welt wäre aber auch gar nichts, was die beiden miteinander zu tun hätten. Da haben sie sich geschnitten, sonst nichts.

Beide Partner können aber auch ihr Kreisdasein als simple Selbst-Konstanz aufgeben und einen gemeinsamen Raum definieren. Wenn sie genug füreinander „brennen“, schaffen sie sich neu aus Brennpunkten und verlagern ihre Mitte vom Mittelpunkt ihres eigenen Selbst weg, in vierfach verschiedener Art:

– als konstante Summe, das gibt eine Ellipse.
In stetiger Rechnung: vergrößert der eine seine Reichweite um ein bestimmtes Maß, verkleinert der andere seine ums gleiche. (Der Abstand vom Brennpunkt zu einem Punkt der Form ist hier Reichweite genannt, mag sie einfach als Armlänge oder Ausdehnung, vielleicht auch als Anstrengung gesehen werden.)
Als Summe, zusammen, sind die Reichweiten überall gleich, werden sie eine gemeinsame Form. Von außen nur noch gemeinsam zu begreifen, nichts unterscheidbar Individuelles gibt es mehr, außer den beiden Brennpunkt-Kernen. Symbiose.
Mit zwei möglichen Extremen: Haben die Brennpunkte fast keinen Abstand mehr, erscheint auch fast wieder ein Kreis mit Doppelpunkt als Zentrum. Wird der Abstand zu groß, zerreißt die Form über die gespannte Linie hinaus ins Nichts – nur die zwei Kerne bleiben, hüllenlos, einsam.

– als konstante Differenz, das gibt eine Hyperbel. Differenzen scheinen ja durchaus sehr oft bestimmend. Ist das die Form der Realität?
Beider Reichweite wächst stetig und gleich oder schrumpft genauso weit.
Die gemeinsamen Differenzen sind überall gleich, das definiert die Form.
Von außen kaum als eine einzige Form zu erkennen, halten die zur Unendlichkeit gestreckten Arme der beiden Hyperbel-Äste ein Streit-X zwischen sich. Dem Anschein nach zwei getrennte Äste, auseinander strebend, zwar die Brennpunkte einander nah. In Wirklichkeit ist der linke Arm des einen Astes der Rechte des anderen…
Die möglichen Extreme: Ist die Differenz gleich Null, erscheinen zwei Raumhälften mit einer graden Grenze zwischen sich, innere Trennung? Ist die Differenz dem Brennpunktabstand gleich, fallen die Ast-Arme, die armen, im Rücken je zur Linie zusammen, verschwindet alle Fülle. Gar keine Hülle gibt es mehr, wenn größer die Differenz. Dann bleiben wie im Falle der Ellipsen nur isolierte Kerne übrig.

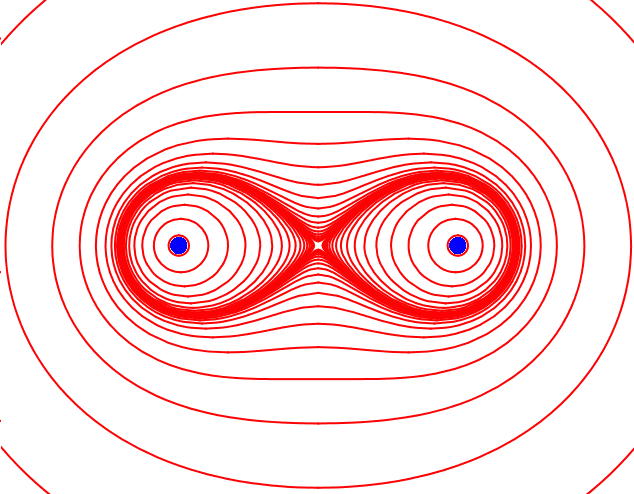
…schaffen sie sich neu aus Brennpunkten – als konstantes Produkt, die Cassinischen Kurven. Hier befinden sich beider Reichweiten in dynamischem Verhältnis zueinander, vervielfacht einer seine, verringert der andere seine um den gleichen Faktor.
Ist das Produkt sehr klein oder sind in Relation die Brennpunkte sehr fern, erscheinen fast einzelne Kreise, nur eine leichte Zuneigung der Hüllen ist ahnbar. Die Zuneigung wächst mit größerer Nähe, es entstehen zwei Eiformen mit deutlichem Bezug. Eine Mitte zwischen den beiden als drittes Zentrum wird spürbar. Die je zugehörigen Hüllformen dehnen sich hin zum gemeinsamen Zentrum, allerdings liegen die Brennpunkte abgewandt. Weiter folgt die Lemniskate, die liegende Acht, unendliches Kreiseln umeinander herum, faszinierend, hier entstehen Achterbahngefühle, eindeutig!
Noch weiter entsteht sozusagen eine eingedellte Ellipse. Hier ist interessant, wie von außen beides erlebbar ist, die Zweiheit genauso wie die Gemeinsamkeit auch, diese durch den Kreuzungspunkt der Acht markiert, der noch spürbar. Am Ende steht fast ein gemeinsamer Kreis um einen Doppelpunkt herum, ähnlich wie selbigen Falles bei der Ellipse.

– als konstante Division, gleichbleibendes Verhältnis, das sind Divisionskreise. Ja, doch, wieder Kreise! Ein Wunder, die Kreise des Apollonius.
Kreise, gebildet ohne Mittelpunkt, die entstehen als Form eines konstanten Verhältnisses!
Die freilich auch einen auffindbaren Mittelpunkt haben, welcher Kreis hätte ihn nicht…
Hier muss ein wenig ausgeholt werden.
Anders als eine Ellipse, Hyperbel oder Cassinische Kurve ist ein einzelner Divisionskreis nicht nur von zwei ganz bestimmten Brennpunkten aus bildbar. Sondern von allen! Klar, er ist eben ein Kreis, drum allseitig gleich. Was bedeutet, dass es zu jedem inneren (Brenn-)Punkt einen äußeren gibt, mit dem zusammen der Kreis gebildet werden kann. Auf diese Weise hat ein Kreis Beziehung zur ganzen Ebene, zu jedem Punkt. Wodurch der Kreis die gesamte Außenwelt in sich hinein spiegelt und umgekehrt! Nicht mehr Banalität und Einsamkeit oder absolute Beziehungslosigkeit gehören zu diesem Kreis, sondern geradezu vollständige Verbundenheit mit der ganzen Welt.
Ein vollständiger Divisionskreis hat freilich immer einen Partner, einen gleichgroßen, symmetrisch. Und zwei Partnerkreise zusammen haben selbstverständlich ein Paar ganz bestimmter Brennpunkte.
Aber jeder beliebige gleichgroße Kreis kann zu einem Partnerkreis werden!
Rücken nur beide Selbste sozusagen ihre Zentren je von ihrem Mittelpunkt ein wenig ab und zueinander hin, bilden diese als einander zugewandte Brennpunkte nun genau ihre zwei eigenen Kreisformen neu. Als Divisionskreise können sie ihre ganze Eigenform vollständig behalten! Äußerlich erscheinen sie unverändert, vollständig und rund. Keiner muss sich verbiegen.
Je weiter entfernt voneinander die beiden Partnerkreise liegen, umso dichter liegen die Brennpunkte an den Mittelpunkten. Je näher aneinander sie sich befinden, umso exzentrischer müssen sie werden, um sich gemeinsam als Divisionskreispaar neu zu bilden. (Im Bild ein Schiel-Effekt.)
Zum Mittelpunkt selbst ist der Partner der unendlich ferne Punkt, in jeder Richtung! Das ist Gott.

Das letzte Bild scheint mir die höchste Möglichkeit zu reflektieren, vollständigste Beziehung zueinander, geradezu Neubildung beider als Partner.
Äußerlich ist das nicht sichtbar, in der Außenform ist keine Neigung erkennbar, keine Verbiegung, keine Deformation. Allein, dass einer neben seinem eigenen Mittelpunkt deutlich brennt, einen Brennpunkt hält, aus dem er zusammen mit dem eines Partners beider Sein definiert, bestimmt den Partnerkreis eindeutig.

Peter Zimmer, 11.7.2013