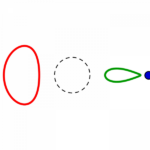
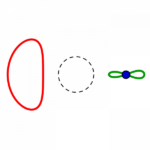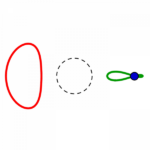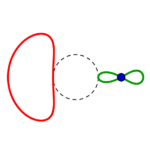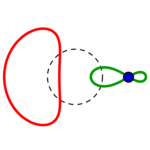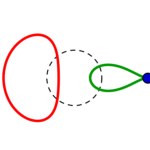Pascalsche Schnecken, Prinzip technisch:
Eine Gardinenstange sei mit einem Punkt an einem drehenden Rad fixiert. An einem andern Punkt rutscht sie über ein Gleitlager. Irgendwo daran sind farbige Stifte fest montiert, die dann zeichen, Löffel, die rühren, Lämpchen, die Leuchtspuren malen:
(Alle Geogebras zum Thema gibt es hier als Arbeitsblätter zum Download.)
Pascalsche Schnecken, Prinzip, animiert:
Starte die Animation und halte sie wieder an (Button unten links), verändere den Betrag der Projektion, erkunde mögliche „Zustände“, prüfe die unten erwähnten 5.
Fasse mit „Fixdrehbar“ den auf der Kreisscheibe fixierten Punkt und drehe das Rad sozusagen von Hand – sieh, wie die Formen entstehen und fühle die unterschiedlichen Geschwindigkeiten!
Verschiebe manuell das Gleitlager auf der Horizontalen, untersuche besonders die beiden heiklen Stellen, wo das Gleitlager den Kreis selber trifft, dort also ein Punkt auf einen Kreis abgebildet wird, also überschlägt auf einen Kreis mit „höchst geringer Punktdichte“ …
Ob so etwas schon mal Anwendung in irgend einem Getriebe fand? (Von den heiklen, technisch unmöglichen Stellen mal abgesehen?) Als lermniskatisches Rührwerk oder so? Vielleicht bei kinetischen Kunstwerken von Tinguely? (Beim Besuch im Museum in Basel dies Jahr war nichts zu finden, leider.) Einzig eine Uhr fand ich bisher als Anwendung.
Pascalsche Schnecken, was sind sie also?
Anders gesagt, wird ein Kreis projiziert, umgewandelt, verschoben: jeder seiner Punkte wird von einem festen Punkt aus (das Gleitlager!) um einen bestimmten Betrag weggepustet oder zu diesem herangesogen, möglicherweise durch diesen hindurch und darüber hinaus.
Diese Art Projektion kann ich von anderen Projektionsarten unterscheiden:
- Zum Beispiel kann eine Lichtquelle ein räumliches Drahtgebilde auf eine Leinwand projizieren, da entsteht ein flächiges Schattenbild: Jeder Punkt des Gebildes wird unterschiedlich weit projiziert, höchstens die Unschärfe des Schattens gibt am Ende Auskunft über die Nähe zur Lichtquelle. (Aus unserem Kreis als Kugel gedacht würde bei quergestellter Leinwand als Schatten eine Kreisscheibe.)
- Ein Geometer kann eine Gebilde so projizieren, dass jeder Punkt auf den z.B. doppelten Abstand zum Projektionspunkt (der „Lichtquelle“) verschoben wird – so entsteht ein Gebilde von gleicher Gestalt aber anderer Größe. Man kennt das als zentrische Streckung/Stauchung. (Aus unserem Kreis würde einfach ein Kreis resultieren.)
Bei der Projektion um einen bestimmten Betrag ändert sich die Gestalt, wie man hier sehen kann. Außer in vier Fällen:
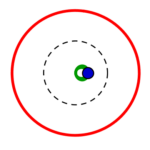
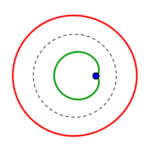
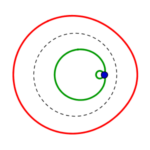
- Sitzt der feste Punkt (das Gleitlager) in des Kreises Zentrum und wird jeder von dessen Punkten um einen bestimmten Betrag weggepustet, entsteht wieder ein Kreis, konzentrisch gestreckt, das ist klar. Ein größerer Kreis ist das Ergebnis.
- Wandert der Punkt (das Gleitlager) nun nach rechts in die unendliche Ferne, wird der Ursprungskreis dann parallel nach links gepustet. Ein gleichgroßer parallel verschobener Kreis.
- Von rechts draußen gepustet, von links außen gesogen, das bleibt sich gleich: Einen Schritt weitergewandert wird gleich der Punkt als Saugquelle im weiteren von links sich nähern: Der gleiche parallel verschobene Kreis ist das Ergebnis.
- Zurück im Zentrum gibt´s wieder einen konzentrischen Kreis, gestaucht diesmal, nach innen gesogen, kleiner? Vielleicht zwar durch den Punkt und über ihn hinaus gar größer…
Formprinzip, 5 Reihen:
5 verschieden Verschiebebeträge sind grundsätzlich nur möglich:
- größer als der Kreisdurchmesser,
- diesem gleich,
- zwischen Durchmesser und Radius,
- letzterem gleich oder
- kleiner.
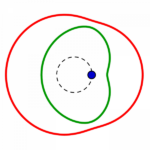
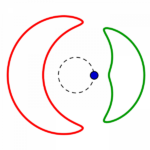
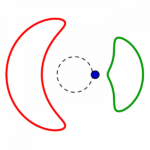
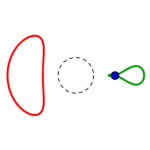
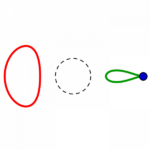
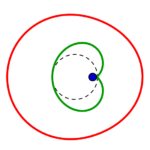
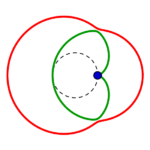
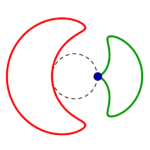
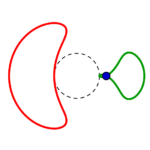
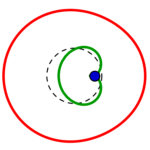
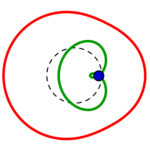
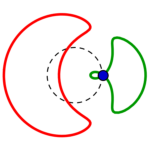
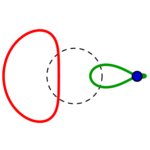
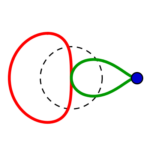
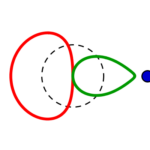
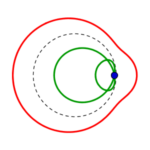
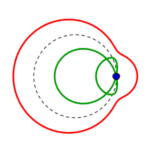
Fünf unterschiedliche Formreihen gibt es also, in jeder gibt es wie oben beschrieben je vier Kreise:
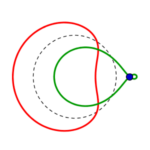
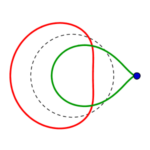
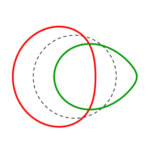
die Reihen beginnen mit einem konzentrisch gestreckten roten links, führen zu einem parallel verschobenen und also immer gleichen roten Kreis rechts, welcher in gleicher Form wie der grüne parallel verschobene von rechts nach links zu einem konzentrisch eingezogenen wird.
(Im Prinzip setzt sich je die rote Reihe so fort, wie die grüne es in umgekehrter Richtung zeigt. Aber die beiden Formen gehören zusammen, an den Stellen, in denen ein Kreis ausgesondert und überschlagen wird, wird das sichtbar.)
Zwischen diesen vier Stationen aber gibt es einen unglaublichen Formreichtum:
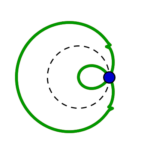
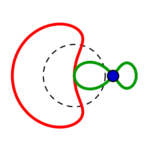
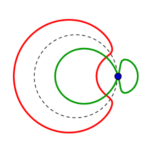
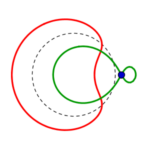
Kreise wandeln sich, schnüren sich ein von oben wie unten, sondern einen kleineren Kreis aus sich heraus
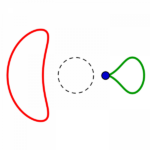
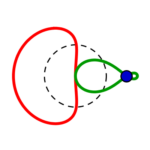
– (am schönsten zu sehen in Reihe 3, 5. Bild. (4. Reihe, 5. Bild zeigt eine ganz ins grüne überschlagene Mischform ohne die zwei Kreishälften!)) –
und werden so zu Monden. Diese zu Bananen, dann Bohnen, breiten assymetrischen Ovalen, wieder Kreisen! Und (grün zurück) weiter schmälern sich diese zu Fast-Ellipsen, dann Eiformen, Tropfen. Schnüren sich Lemniskatisch ab, lassen einen Teil zum Nasenmond werden, schlagen über den Kreis auf die andere Seite hinüber und zeigen embryonale Einstülpungen, die sich wieder zum Kreis auflösen…
Alle Formen sind Umwandlungen des einen Kreises, aus allen Formen lässt sich natürlich umgekehrt auch derselbe eine Kreis projizieren!
Der Kreis, rückwärts aus diesen Gebilden geformt:
Alle diese roten und grünen Formen sind Umwandlungen des einen gestrichelten Kreises – aus allen diesen Formen lässt sich natürlich umgekehrt auch derselbe eine Kreis projizieren! (Der Kreis als Ergebnis der Projektion von einer ganz anderen Form aus.)
Im Arbeitsblatt unten lässt sich das durchspielen: Die grüne Form ist durch die bekannte Projektion über das Gleitlager aus dem grauen Originalkreis gebildet (- In der obersten der 5 Reihen ist sie im zweiten Bild seitenverkehrt in grün in etwa wiederzuerkennen).
Mit gleichem Projektionsradius ist diese grüne Form über das Gleitlager_2 auf die magentafarbene Form projiziert (- wie oben die grünen manchmal in die roten umschlagen, so diese in die orange – drum ist sie gleich mitgezeichnet).
Liegt das zweite genau auf dem ersten Gleitlager, muss natürlich als Ergebniskreis der Originalkreis wieder herauskommen, im Bild liegt er zunächst auf dem grauen Kreis, diesen verdeckend.
Aber als Sonderform welcher Formfamilie entsteht hier der Kreis? Bewege das Gleitlager_2 und sieh, aus welcher Formenwelt als Spezialfall der Kreis erscheint, bewege es auf der Linie oder frei in der Fläche, bewege auch „Fixdrehbar“:
Pascalsche Schnecken von fünferlei Form in einem:
Hier sind die fünf Möglichkeiten in einem Arbeitsblatt versammelt. Verschiebe den „blauen Punkt“ oder verändere den Radius, lasse den Projektionspunkt durch Verstellen der Geschwindigkeit nach rechts oder links wandern.
Pascalsche Schnecken, Spur, Punktdichte:
Schaue, wie unterschiedlich dicht die Punkte liegen, wie „dünn sie gesät“ sind in unmittelbarer Nähe zum Um- oder Überschlagskreis – jenem Kreis, auf den der eine Punkt projiziert wird, wenn der Gleit- oder Projektionspunkt genau auf der Kreislinie liegt.
Weitere Möglichkeiten
– im weiteren habe ich angenommen, jemand würde Getriebe bauen solcher Art. Löffel solche Formen rühren lassen. Lampen solche Spuren zeichnen lassen.
Dann habe ich gewissermaßen an dem „Löffelpunkt“ wiederum die nächste Gardinenstangen befestigt, durch einen weiteren Punkt gleiten lassen, einen weiteren Löffel befestigt und gleichzeitig wiederum die nächste Gardinenstange usw..
Auch Scheiben auf der Stange befestigt und die Lampe neben der Stangenlinie ihre Spur zeichnen lassen (in bestimmtem oder kreisenden Winkel zur Gardinenstange). Oder so.
Damit der Browser nicht überlastet wird, habe ich die weiteren meditativen Geogebras auf einem Extrablatt versammelt: Klick! Wer mag, kann sich das Blatt per Rechtsklick in neuem Tab daneben öffnen.