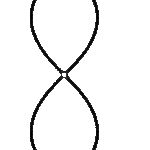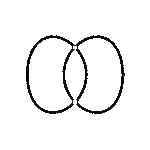Cassinische Kurven & Divisionskreise

Für die Kegelschnitte – Ellipsen und Hyperbeln zusammen – ist ein schöner Gang gefunden, welcher in seinen Gestaltwandlungen sehr nah an eine echte Metamorphose kommt.

Ob sich ein solcher metamorphosischer Gang durch die Cassinischen Kurven finden lässt?
Vielleicht gar zusammen mit den Divisionskreisen?! – Ein Gang durch Kreise ist aber per se schon wenig interessant – welch interessante Eigenart dieser in ihrem Sein so interessanten Form, dass es ihr sonst an aller Interessantheit mangelt!

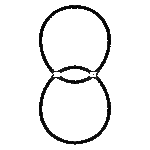
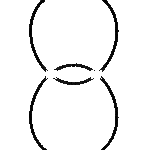
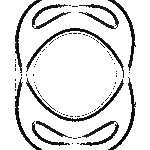
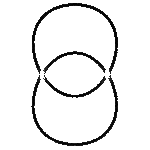
Den einen Gang zeigen die Bilder der Kreisscharen: die Brennpunkte sind fest, das Produkt wächst, das gibt eben die bekannte Schar der Cassinischen Kurven, welche in sich ja schon eine große Differenzierung aufweisen. (Und die zugehörigen Divisionskreise erscheinen mit.)

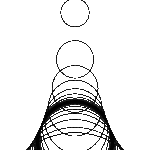
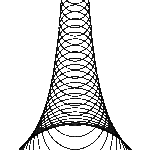
Unten ist spaßeshalber die dem „Gang durch die Kegelschnitte“ entsprechende Konstruktion versucht (Scheitelgleichung). Ein Brennpunkt und ein Berührpunkt (Scheitelpunkt) sind fest gesetzt, der zweite Brennpunkt wird auf die Reise geschickt…

Geogebra macht´s möglich. (Die Geogebras als Arbeitsblätter gibt es zum Download hier!)

Interessant dabei scheint mir zweierlei:

• anders als bei den Kegelschnitten wird nicht die ganze Fläche ergriffen, alles spielt sich zwischen den Höhen jener Form ab, die bei positiver Geschwindigkeit zunächst rechts entsteht als Langoval mit Flachstellen oben und unten.
• Dreimal tritt die Lemniskate auf in diesem Gang! Und so auch alle anderen möglichen Cassinischen Gestalten, alle geteilten wie auch geschlossenen Ovale.
  Unten gibt es das gleiche Geogebra mit dreifachem zweiten Brennpunkt, die drei Punkte so voreingestellt, dass alle drei Lemniskaten sichtbar sind:

Die Kreisscharen zeigen je die Verwandtschaft, die der Ellipsen mit den Hyperbeln und die der Cassinischen Kurven mit den Divisionskreisen. Jedoch gibt es einen wesentlichen Unterschied dieser beiden Verwandtschaften.

• Weil eine Summe mit einem Negativen eine Subtraktion ist, finden sich alle Kegelschnitte im ganzen Rundgang eines Brennpunktes. Geht der eine Brennpunkt aus dem positiven Bereich durch die Unendlichkeit in den negativen über, so wechseln – sozusagen natürlich – die Formen aus den Ellipsen per Parabel in die Hyperbeln.
• Das Produkt mit einem Negativen jedoch ist nicht eine Division – anders als bei den Kegelschnitten gehen die Cassinischen Kurven nicht in die Divisionskreise über beim ganzen Rundgang eines Brennpunktes.

Gibt es eine Bewegung, bei welcher die Produktbildung in eine Division übergeht? Diese Frage mag mathematisch unsinnig erscheinen. Vom Aspekt der Gestaltwandlungen her fühlt sie sich relevant an. Und man ahnt, dass vielleicht die Potenzen damit zu tun haben werden, zwar nur bei einem ganz bestimmten „Faktor“ ergibt sich bei einer Potenz mit Exponent größer 1 etwas „produktives“, bei einer solchen mit Exponent kleiner 1 etwas „divisionäres“. Hier teilt sich die Welt qualitativ in Innen und Außen. Der Negation entspricht eher die Inversion, wer weiß.

Zur Betrachtung der Verwandtschaft hier ein Geogebra mit Cassinischer Kurve und Divisionskreis so, dass beider Konstanten gleich sind, Produkt wie Quotient. Verändere per Schieberegler diese Konstante und beachte die interessanten Stellen (Leider werden Geogebras Reaktionen nur bei leichten Scrollbewegungen sichtbar):

Höhenlinien

Es gibt ein Gebiet, auf dem den Cassinischen Kurven ähnliche Gebilde in vielen Variationen und Abwandlungen vorkommen, jede Landkarte zeigt solche. Hier sind ein paar Beispiele aus dem Netz versammelt: 1, 2, 3, 4, 5, 6, 7, es gibt sogar einen Test dazu. Man kann schön sehen, wie der cassinischen Kurven prägnanteste Form: die Lemniskate, dem Sattel oder Pass als Geländeformation entspricht und damit die Qualität der „doppelt gebogenen Fläche“ ins Bild setzt – am Pass muldet sich die Fläche konkav von einem Gipfel zum anderen, sie wölbt sich konvex von einer Talseite hinüber auf die andere.

Es gibt eine Webseite, welche sehr differenzierte Cassiniennes auf französisch (ma)thematisiert, darauf oben ein sehr Höhenlinienähnliches Gebilde.

Und Isobaren zeigen ganz ähnliche Formtendenzen, nicht Linien gleicher Höhe, sondern gleichen Luftdruckes.

Unten kann man eine „Ebene mit 5 Gipfeln“ selber verändernd durchspielen indem man das Tempo ungleich Null setzt:

Allerdings sind die „Hügel dieser Landschaft“ ideal, d.h. sie ergeben sich so, als würden nur Kräfte polar zu einer ganz homogenen „Haut“ diese aufwölben oder einmulden. Auf jeder Landkarte sieht der kundige Leser unterschiedliche „Haut-Härten“, seitliche Kräfte (Böschungen von Prall- und Gleithang!), vielerlei weitere Faktoren, die ein Landschaftsbild bestimmen.

Die Cassinischen Kurven und besonders die Lemniskate haben immer schon viele Menschen begeistert, sie werden auch von den Anthroposophen hochgeschätzt. Hier sind Rudolf Steiners Ausführungen dazu schön versammelt. Man kann sie auch selber im Kontext finden bei der Steinerdatenbank fvn-rs.net. Interessant finde ich vor allem die freie Betrachtung der Lemniskate als Schleifenbildung, da hier sogar ausdrücklich ein Bezug zu den Zykloiden und damit auch den Pascalschen Schnecken gesetzt wird.

Zuletzt noch eine Bilderreihe von Formfamilien, welche aus Variationen der (Exponenten der) allgemeinen Koordinatengleichung der Cassinischen Kurven entstand ((x²+y²)² – 2c² (x²-y²) – a⁴ + c⁴=0):